Centre de gravité - Barycentre

Formulaire de report

Problème d'affichage Contenu de la note peu pertinent

Définition

Centre de gravité d'un triangle : point de ce triangle où passent les droites qui passent par un sommet et coupent le côté opposé en son milieu


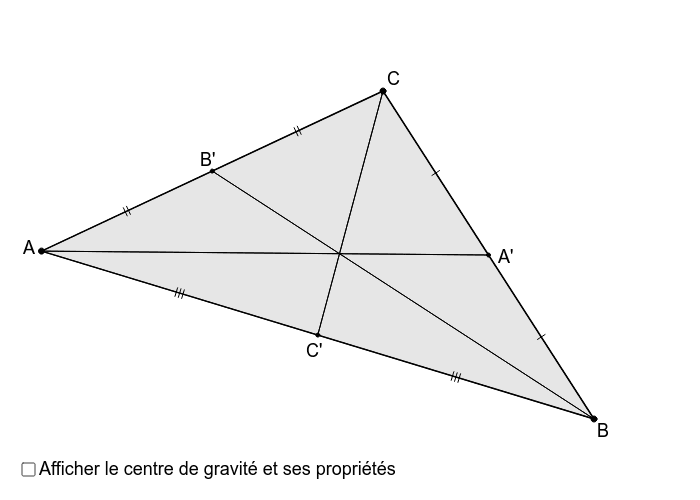
(Triangle, Médiane)

Consigne: Soit \(\triangle ABC\) un triangle non dégénéré
Montrer que les trois hauteurs sont concourantes
On appelle centre de gravité ou barycentre leur point d'intersection

Hauteurs se coupent car ce sont les médiatrices d'un autre triangle

Les parallèles à \((AB)\) passant par \(C\), \((BC)\) par \(A\) et \((CA)\) par \(B\) forment un triangle dont les médiatrices sont les hauteurs de \((ABC)\) \(\Rightarrow\) elles se coupent

Intérêt

Le centre de gravité d'un triangle marque le point qui serait le centre de masse si ce triangle était découpé dans un matériaux uniforme

(Théorème du centre d’inertie)